Learning Concepts in C++ Part 3: Groups

last edited on 2023-09-28

link to repository https://github.com/jgsuw/math_concepts_cxx

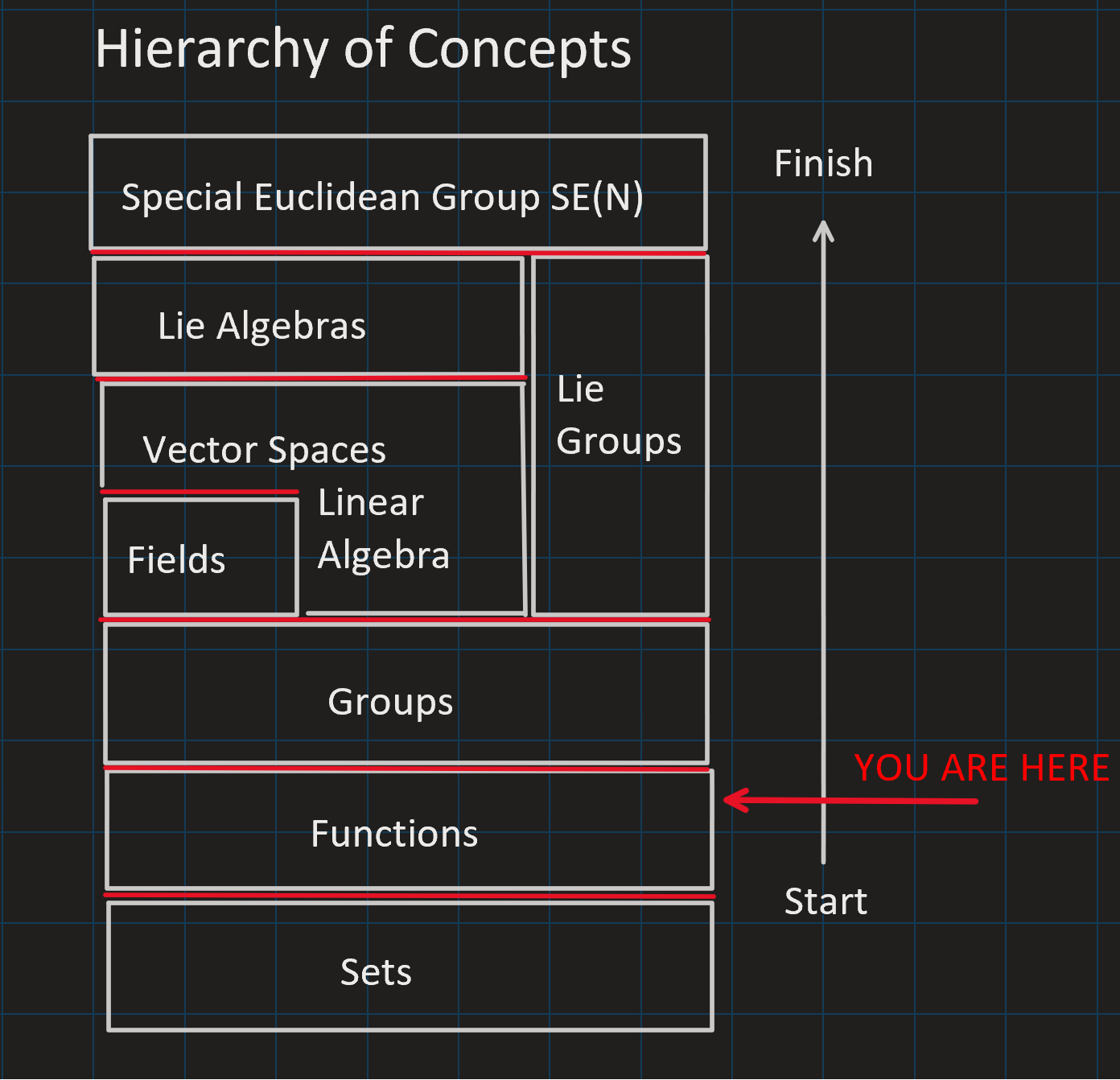
On the path to \(\text{SE}(3)\)

As part of a project to learn how to use Concepts and Templates in C++, I set out on a path towards implementing a template library for \(\text{SE}(3)\). In my previous post, I introduced the PointSet concept and implemented template classes for NaturalNumbers, Integers, RationalNumbers, and RealNumbers. However, there are many more concepts to define before I have an implementation of \(\text{SE}(3)\). An essential property of \(\text{SE}(3)\) is it carries a group structure, and so we need a concept for this property.

What’s in a Group?

A group is a set \(X\) with a closed binary operation \(f : X \times X \to X\) which satisfies the following axioms:

• Existence of identity: \(\exists \text{id} \in X : \forall x \in X : f(x,\text{id}) = f(\text{id},x) = x\)
• Existence of inverse: \(\forall x \in X : \exists y \in X : f(x,y) = f(y,x) = \text{id}\)
• Associativity: \(\forall x,y,z \in X : f(x, f(y,z)) = f(f(x,y), z)\)

That is, \(\forall x,y,z \in X : f(x,f(y,z)) = f(f(x,y),z)\). We can use PointSet as a stand-in concept for \(X\) being a set. But a new concept is needed to represent the group operation \(f\).

Concepts for Functions & Binary Operators

First I introduce a concept for a general function,

template <class F>
concept Function = 
    PointSet<typename F::Domain> &&
    PointSet<typename F::Target> &&
requires(F::Domain::type& x, F::Target::type& y) {
  y = F::apply(x);
};

Function requires that class F has properties Domain and Target that satisfy the concept PointSet. It further requires that the argument of F::apply has Domain::type and the return value has Target::type. It would be nicer to overload F::operator()() instead of having F::apply, but unforunately operator() cannot be statically overloaded. Next we build upon PointSet and Function to make BinaryOperator and ClosedBinaryOperator concepts.

Our requirements for BinaryOperator should be that it is a Function whose Domain is a Cartesian Product of two sets. The requirements for ClosedBinaryOperator will be the the requirements for BinaryOperator plus a constraint on the Target of the function.

template <class F>
concept BinaryOperator = 
            Function<F> &&
requires (F::Domain::type& x) {
    x.first;
    x.second;
};

template <class F>
concept ClosedBinaryOperator = BinaryOperator<F> &&
        std::same_as<typename F::Domain::type::first_type, 
            typename F::Domain::type::second_type> &&
        std::same_as<typename F::Domain::type::first_type, 
            typename F::Target::type>;

In BinaryOperator we require that Domain::type behave like a std::pair.

Satsifying the Group Axioms

Next we need concepts that implement the identity and inverse axioms of the group. These we will call HasIdentityElement and HasInverseElement:

template <class F>
concept HasIdentityElement = ClosedBinaryOperator<F> && 
requires (F::Target::type& x) {
    F::has_identity(x);
};

template <class F>
concept HasInverseElement = ClosedBinaryOperator<F> && 
requires (F::Target::type& x) {
    F::has_inverse(x);
};

At this point it is important to observe that the concepts HasIdentityElement and HasInverseElement only requires that our ClosedBinaryOperator candidate class F has static functions named has_identity and has_inverse with the correct signature. These will need to be implemented, and should be written so as to test their corresponding axioms:

• Existence of Identity: \(\exists \text{id} \in X : \forall x \in X f(\text{id},x) = f(x,\text{id}{x}) = x\)
• Existence of Inverse: \(\forall x \in X : \exists y \in X f(x,y) = f(y,x) = \text{id}\)

The first statement requires a identity that holds for every element of the group, and the second axiom requires every element has an inverse. Unfortunately, these axioms are predicates which cannot be checked by the compiler because in general the underlying set may be ifinite or even uncountable. This points to a fundamental limitation of what can be accomplished with concepts in C++ : concepts and templates are no substitution for mathematical proofs.

Finally, the group operation also needs to be associative. For a binary operator to be associative, it must satsify a predicate that quantifies over the set \(X\). Recall the associativity axiom for groups,

• Associativity: \(\forall x,y,z \in X : f(x, f(y,z)) = f(f(x,y), z)\)

In this logical formula, the symbol \(\forall\) is a quantifier, \(\forall x,y,z \in X\) is a quantification over the set \(X\) which in plain English means “for every trio of elements in the set \(X\),”. Like wth the identity and inverse axioms, the quantification over \(X\) in the associativity axiom results in a predicate which cannot be checked by the compiler.

Despite this it would still be preferable for associativity to be represented in a concept. The solution I have settled on is essentially to make the code “swear under oath” that it satisfies the associativity predicate. For instance

template <class F>
concept Associative = ClosedBinaryOperator<F> && 
requires (F::Target::type& x, F::Target::type& y, F::Target::type& z) {
    F::is_associative(x,y,z);
};

This requires that class F has a static function is_associative which should test the associativity axiom given some \(x,y,z\). In this way, class F tells the concept “I am associative” even though it could not be. We now possess all concepts for all the axioms that are required for a Group concept.

template <class Set, class Op>
concept Group =
        std::same_as<Set, typename Op::Target>
        HasIdentityElement<Op> &&
        HasInverseElement<Op> &&
        Associative<Op>;

Later on, we will want to construct the field of Real numbers, which behaves as an Abelian group under addition and multiplication. Abelian groups are groups that satisfy one addtional axiom:

• Commutativity: \(\forall x,y \in X : f(x,y) = f(y,x)\)

Like with associativity, this is not a predicate which the compiler can actually evaluate, so we will make our template “swear” to an AbelianGroup concept that their operation is commutative.

Example Group Template - \((\mathbb{R}, +)\)

To instantiate our first group, we look to define addition on our RealNumbers template from before.

template <typename T>
class RealAddition {
public:
    using Domain = CartesianProduct<RealNumbers<T>,RealNumbers<T>>;
    using Target = RealNumbers<T>;

    static inline T identity() { return RealNumbers<T>::zero; }
    static void has_identity(const T& x) { 
        static_assert(apply(identity(), x) == x);
    }

    static inline T inverse(const T& x) { return -x; }
    static void has_inverse(const T& x) { 
        static_assert(apply(inverse(x),x) == identity());
    }

    static inline T apply(const T& x, const T& y) { return x+y; }
    static inline T apply(const Domain::type& x) { return x.first+x.second; }

    static void is_commutative(const T& x, const T& y) {
        static_assert(apply(x,y) == apply(y,x));
    }
    static void is_associative(const T& x, const T& y, const T& z) {
        static_assert(apply(x,apply(y,z)) == apply(apply(x,y),z));
    }
};

The CartesianProduct template type was added to wrap std::pair into a class that satisfies the PointSet. At this point things are getting more abstract and removed from the basic concept building blocks, and so it seems like a good time to make an accounting of what the compiler will do when we try to constrain the RealAddition template according to our Group concept. For this, we have a test function that we will test on RealAddition<float>

template <class Set, class Op>
bool is_AbelianGroup() { return AbelianGroup<Set,Op> }

using Set = RealNumbers<float>;
using Op = RealAddition<float>;

int main(void) {
  if (is_AbelianGroup<Set, Op>()) return 0;
  return -1;
}

When we compile this code, the concrete type RealAddition<float> will be checked against the chain of concepts we have imposed on AbelianGroup. Starting from the top-level concept, the following concepts (among a few others) will be checked:

• AbelianGroup<Set, Op> requires Group<Set, Op>
  • Group<Set, Op> requires Associative<Op>
    • Associative<Op> requires ClosedBinaryOperator<Op>
      • ClosedBinaryOperator<Op> requires BinaryOperator<Op>
        • BinaryOperator<Op> requires Function<Op>
          • Function<Op> requires PointSet<Op::Domain> and PointSet<Op::Target>

Similarly, we can define a template class RealMultiplication<T> which satisfies the group axioms, which is will be required to define a Field concept needed for a later VectorSpace concept.